二次函数对称轴公式是什么，二次函数的对称轴公式是什么? _二次

二次函数对称轴公式是什么
二次函数对称轴公式：x=-b/2a 。二次函数的基本表示形式为y=a（x的平方）+bx+c（a不等于0）。二次函数最高次必须为二次，二次函数的图像是一条对称轴与y轴平行或重合于y轴的抛物线。
二次函数表达式为y=a（x的平方）+bx+c（a不等于0），它的定义是一个二次多项式（或单项式）。
如果令y值等于零，则可得一个二次方程。该方程的解称为方程的根或函数的零点。
二次函数的历史：
大约在公元前480年，古巴比伦人和中国人已经使用配方法求得了二次方程的正根，但是并没有提出通用的求解方法。公元前300年左右，欧几里得提出了一种更抽象的几何方法求解二次方程。
7世纪印度的婆罗摩笈多是第一位懂得用使用代数方程的人，它同时容许有正负数的根。
11世纪阿拉伯的花拉子密独立地发展了一套公式以求方程的正数解。亚伯拉罕巴希亚（亦以拉丁文名字萨瓦索达著称）在他的著作Liber embadorum中，首次将完整的一元二次方程解法传入欧洲。
据说施里德哈勒是最早给出二次方程的普适解法的数学家之一。但这一点在他的时代存在着争议。这个求解规则是：在方程的两边同时乘以二次项未知数的系数的四倍；在方程的两边同时加上一次项未知数的系数的平方；然后在方程的两边同时开二次方（引自婆什迦罗第二）
二次函数的对称轴公式是什么?二次函数的对称轴公式是x=-b/2a 。
二次函数的基本表示形式为y=ax2+bx+c（a≠0）。二次函数最高次必须为二次，二次函数的图像是一条对称轴与y轴平行或重合于y轴的抛物线。

函数性质
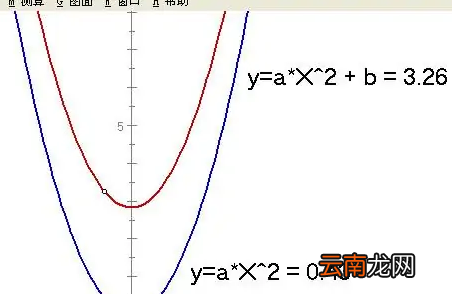
1、二次项系数a决定抛物线的开口方向和大小。
当a>0时，抛物线开口向上；当a<0时，抛物线开口向下；
|a|越小，则抛物线的开口越大；|a|越大，则抛物线的开口越小。
2、一次项系数b和二次项系数a共同决定对称轴的位置。
当a与b同号时（即ab>0），对称轴在y轴左侧；
当a与b异号时（即ab<0），对称轴在y轴右侧。（可巧记为：左同右异）
3、常数项c决定抛物线与y轴交点。抛物线与y轴交于(0, c）。
二次函数的表达式
1、顶点式
y=a(x-h)2+k(a≠0,a、h、k为常数)
2、交点式

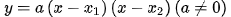
二次函数对称轴公式设二次函数的解析式是y=ax^2+bx+c
则二次函数的对称轴为直线x=-b/2a,顶点横坐标为-b/2a,顶点纵坐标为(4ac-b^2)/4a
怎样求二次函数的对称轴公式1、对称轴公式是：x=-b/(2a) 。
2、对于二次函数y=ax^2+bx+c
其顶点坐标为(-b/2a,(4ac-b^2)/4a)交点式：y=a(x-x?)(x-x?)[仅限于与x轴有交点A（x?，0）和B（x?，0）的抛物线]
其中x1，2=-b±√b^2－4ac
顶点式：y=a(x-h)^2+k
[抛物线的顶点P（h，k）]
一般式：y=ax^2+bx+c（a，b，c为常数，a≠0）
注：在3种形式的互相转化中，有如下关系:h=-b/2a=（x?+x?）/2k=(4ac-b^2)/4a与x轴交点：x?,x?=(-b±√b^2-4ac)/2a

扩展资料二次函数最高次必须为二次，二次函数的图像是一条对称轴与y轴平行或重合于y轴的抛物线。
二次函数表达式为y=ax2+bx+c（且a≠0），它的定义是一个二次多项式（或单项式）。
如果令y值等于零，则可得一个二次方程。该方程的解称为方程的根或函数的零点。
一般地，把形如（a、b、c是常数）的函数叫做二次函数，其中a称为二次项系数， b为一次项系数，c为常数项。x为自变量，y为因变量。等号右边自变量的最高次数是2 。
顶点坐标：（-b/2a ， (4ac-b2)/4a）。
交点式为y=a(x-x1)(x-x2) （仅限于与x轴有交点的抛物线），
与x轴的交点坐标是A（x1，0）和 B（x2，0）
注意：“变量”不同于“未知数”，不能说“二次函数是指未知数的最高次数为二次的多项式函数” 。“未知数”只是一个数（具体值未知，但是只取一个值），“变量”可在一定范围内任意取值。
在方程中适用“未知数”的概念（函数方程、微分方程中是未知函数，但不论是未知数还是未知函数，一般都表示一个数或函数——也会遇到特殊情况），但是函数中的字母表示的是变量，意义已经有所不同。从函数的定义也可看出二者的差别。
二次函数对称轴的公式二次函数求对称轴的公式是x=-b/2a ，二次项系数a决定抛物线的开口方向和大小。当a>0时，抛物线开口向上；当a<0时，抛物线开口向下。|a|越大，则抛物线的开口越?。粅a|越小，则抛物线的开口越大。
在数学中，二次函数最高次必须为二次，二次函数表示形式为y=ax2+bx+c（a≠0)的多项式函数。二次函数的图像是一条对称轴平行于y轴的抛物线。
二次函数表达式y=ax2+bx+c的定义是一个二次多项式，因为x的最高次数是2 。
如果令二次函数的值等于零，则可得一个二次方程。该方程的解称为方程的根或函数的零点。
二次函数中对称轴的公式是什二次函数y=ax2+bx+c的对称轴公式是：x=-b/(2a)；
顶点坐标公式[-b/(2a)，（4ac-b2)/(4a)].
二次函数中对称轴的公式是什二次函数y=ax2+bx+c的对称轴公式是：x=-b/(2a)；
顶点坐标公式[-b/(2a) ，（4ac-b2)/(4a)].
二次方程的对称轴公式是什么

二次函数的对称轴公式是x=-b/2a 。其中，a表示的是二次函数y=ax^2+bx+c的二次项系数，b是一次项系数，但当二次函数是顶点式y=a(x-h)^2+k时，其对称轴公式是x=h 。
二次函数的相关性质
对于二次函数y=ax^2+bx+c
其顶点坐标为(-b/2a,(4ac-b^2)/4a)交点式：y=a(x-x?)(x-x?)[仅限于与x轴有交点A（x?，0）和B（x?，0）的抛物线]
其中x1，2=-b±√b^2－4ac
顶点式：y=a(x-h)^2+k
[抛物线的顶点P（h，k）]
一般式：y=ax^2+bx+c（a ， b ， c为常数，a≠0）

抛物线的性质
1、抛物线是轴对称图形。对称轴为直线x=-b/2a 。
对称轴与抛物线唯一的交点为抛物线的顶点P 。特别地，当b=0时，抛物线的对称轴是y轴（即直线x=0）
2、抛物线有一个顶点P，坐标为：P(-b/2a ， (4ac-b^2)/4a)当-b/2a=0时， P在y轴上；当Δ=b^2-4ac=0时，P在x轴上。
3、二次项系数a决定抛物线的开口方向和大小。
当a＞0时，抛物线向上开口；当a＜0时，抛物线向下开口。|a|越大，则抛物线的开口越小。
4、一次项系数b和二次项系数a共同决定对称轴的位置。
当a与b同号时（即ab＞0），对称轴在y轴左；
当a与b异号时（即ab＜0），对称轴在y轴右。
5、常数项c决定抛物线与y轴交点。
抛物线与y轴交于（0 ， c）
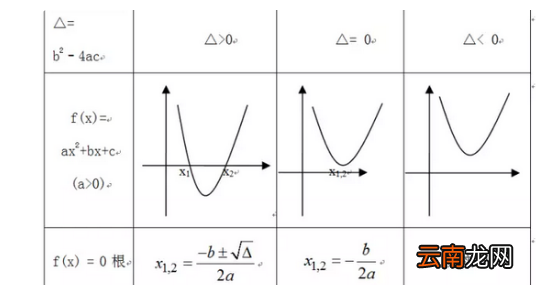
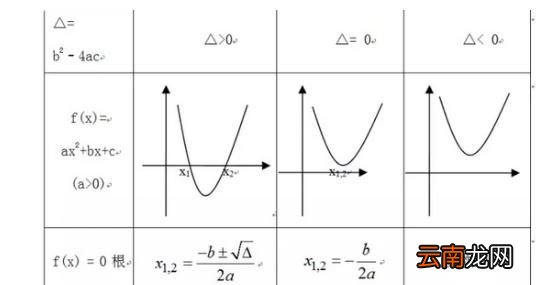
6、抛物线与x轴交点个数
Δ=b^2-4ac＞0时，抛物线与x轴有2个交点。
Δ=b^2-4ac=0时，抛物线与x轴有1个交点。
Δ=b^2-4ac＜0时，抛物线与x轴没有交点。X的取值是虚数（x=-b±√b^2－4ac的值的相反数，乘上虚数i，整个式子除以2a）
怎样二次函数对称轴公式顶点坐标公式1、对称轴公式是：x=-b/(2a) 。
2、对于二次函数y=ax^2+bx+c
其顶点坐标为 (-b/2a,(4ac-b^2)/4a)交点式：y=a(x-x?)(x-x ?) [仅限于与x轴有交点A（x?，0）和 B（x?，0）的抛物线]
其中x1，2= -b±√b^2－4ac
【二次函数对称轴公式是什么，二次函数的对称轴公式是什么?】顶点式：y=a(x-h)^2+k
[抛物线的顶点P（h，k）]
一般式：y=ax^2+bx+c（a ， b ， c为常数， a≠0）
注：在3种形式的互相转化中，有如下关系:h=-b/2a= （x?+x?）/2 k=(4ac-b^2)/4a 与x轴交点：x?,x?=(-b±√b^2-4ac)/2a
扩展知识：