作为一个高中数学老师,首先专业要过硬,就是高中数学本身要过关,只有当老师自己对所讲的内容透彻掌握,觉得直观自然,学生听起来也才容易听懂 。要说大家在学校里对哪个老师印象最深,能有交集、能取得共识的一定也是这个周老师吧!周老师对学生非常好,一是他有一颗仁义之心,宽爱所有的学生,不管是年龄大是年纪小的学生;二是他确实非常认真负责,一心扑在学生身上,帮助学生适应初中生活(因为对我们来说,从小学到初中的确算是一次质的飞跃) 。
高中数学解题思路有哪些?
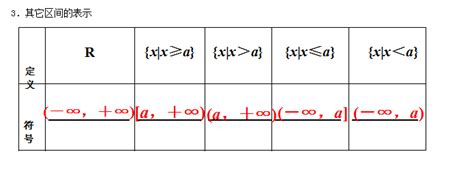
谢邀!这是一个非常大的话题,高中数学题的解题思路或者说解题技巧有很多,比如:配方、换元、参变分离、构造辅助函数、数形结合等等 。这也是学习高中数学时最难掌握的内容,因为这些内容零零散散的散布于数学课本的任何角落,甚至很多技巧在课本上并没有出现,是需要通过大量的题目训练才能见到这些技巧并逐步掌握 。一一列举不是短时间内可以实现的,但我们可以简单的把这些技巧归纳为四大类,从而为你解题提供一个方向,不至于见到题目像无头苍蝇 。
那么有那四大类呢?这就是著名的数学四大解题思想!1. 函数与方程的思想毫无疑问,这是接触时间最早的一个解题思想,初中一年级开始接触的方程,从而再也不为“鸡兔同笼”问题发愁了 。那么函数与方程思想在高中阶段的主要应用包括:要求几个未知数就需要几个方程、函数求值域、函数的单调性等等 。数学题中的求值型问题(例如求参数的值、求曲线的方程等等都是求值型问题),大多数都需要用到函数与方程思想 。
此外,该思想在物理题中的应用非常广泛,比如绳子的拉力随着角度的变化如何变化就是函数的单调性问题,即函数F=f(α)的单调性问题 。2. 分类讨论思想在初中阶段,更多的研究的是确定性问题,而到了高中,更加侧重学生对不确定性问题的解决,比较常见的就是含参数的问题,这个时候就需要进行分类讨论啦,这个思想比较容易理解,就不多做解释了 。
这类问题其实并不可怕,其解决的入手点,就是把参数先改成具体的数值,看自己是否会做,再考虑是不是改成任何数值,其解法和答案的形式都一样呢?从而帮助我们找到分类讨论点以及解决的思路 。若果改成具体的数值你都无法判定是否满足题意,那就赶紧跳过吧:),说明这道题超出了你的能力范围 。3. 数形结合的思想数学结合的思想是帮助我们把一堆数字与字母的结合体,转化成便于理解和思考的图象,从而帮助我们解决问题,因为“看图说话”是我们从幼儿园开始就训练的一项能力,可以避免我们单纯的抽象解决问题 。
比如让求取2m n的取值范围,我们就可以看成求取Z=2x y的取值范围,从而转化为一个线性规划问题,把Z看成一条直线的截距,后面我们会用一道例题来辅助说明 。4. 转化与化归的思想这也是高中阶段解题用的非常多的一个思想,这种思想说白了就是对题目的“再翻译”,把题目中的已知条件和问题翻译的通俗易懂,并且在数学上可操作,比如常见的“恒成立和存在性”问题,某式子大于零恒成立,说白了就是该式子的最小值大于零,“至少有一个如何如何”,可以转化为“一个都没有”来正难则反的解决问题 。
换元法也是转化与化归的思想的典型应用,通过换元的方式,就把一个不熟悉的问题,转化为熟悉的问题 。很多题目都需要一边读题,一边对其已知条件进行转化与翻译,因为出题人不会很直白的告诉你的,总是会添加很多掩饰的东西 。以“范围型(最值型)”问题为例解释说明范围型或者说最值型问题,是大家在高中阶段比较头疼的问题,一看到“求某某的最大值、最小值或者范围”就是属于这类问题,肯定都多多少少的有点难度,肯定不是给你送分的题目 。
推荐阅读
- 如何写数学试卷分析,家长写数学试卷分析
- 小学数学教学中如何培养学生数学情感,如何培养学生学习数学的兴趣论文
- 读数学系毕业后能干嘛,数学系毕业论文写什么
- 试题试卷/课件/教案/教学设计,高中英语的教学设计怎么写
- 这样培养数学学习兴趣,如何培养数学学习兴趣
- 如何构建高效课堂,高中数学如何实现高效课堂
- 选课走班怎么上课,小学走班选课怎么选择
- 如何提高高中文言文课堂效率,提高高中文言文需要读哪些书
- 小学数学论文范文,怎么写科研数学论文
- 怎样提高六年级数学,六年级数学怎么提高












